Looking for a Glass Hearth?
We get asked about Glass hearths regularly as a way of seeing the floor underneath. The only issue is glass conducts heat!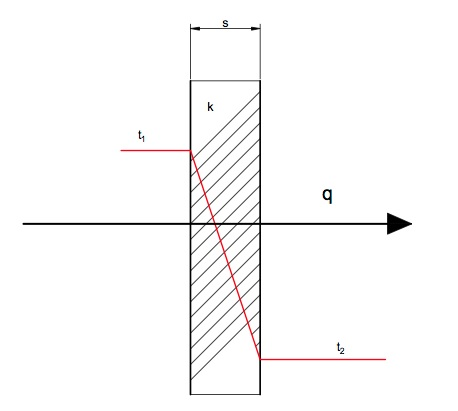
Being the technical specialists that we are instead of just making an assumption we did the maths. See below why it is not a good idea for a glass hearth:
If we use Fourier's law and assuming glass can actually withstand the temperature of a burning log (say 700 degrees C) as most tempered glass have a shock value of 250 degrees C you would be looking at approximately 25 minutes for the sub floor to heat up 90 degrees above ambient:
q = (k / s) A dT
where
q = heat transfer (Watts - This is what we want to calculate)
k = material thermal conductivity rating (it is generally 1.05 for glass)
s = material thickness (9mm = 0.009m)
A = heat transfer area (30 x 30cm = 0.09m2)
dT = t1 - t2
= temperature gradient - difference - over the material (700 - 90 = 610)
Plugging the values into Fourier's Law we get:
= 1.05 / 0.009 * 0.09 * 610
= 6405 Watts
Assuming a 0.5kg log that has fallen out with a calorific energy value of 18MJ/kg (9MJ for 0.5kg) we can convert Watts (J/s) into how many seconds it takes to transfer through which looks like:
= 9000000 (Joules) / 6405 (Joules / Second) / 60 (seconds to minutes)
= 23 minutes
So it takes 23 minutes for a burning log to get the floor underneath to above 90 degrees above ambient when on a 9mm piece of glass assuming it doesn't crack under the temperature first.
Conversely a 10mm FC sheet works out at 1 hour 20 minutes for heat to transfer through.
If we use Fourier's law and assuming glass can actually withstand the temperature of a burning log (say 700 degrees C) as most tempered glass have a shock value of 250 degrees C you would be looking at approximately 25 minutes for the sub floor to heat up 90 degrees above ambient:
q = (k / s) A dT
where
q = heat transfer (Watts - This is what we want to calculate)
k = material thermal conductivity rating (it is generally 1.05 for glass)
s = material thickness (9mm = 0.009m)
A = heat transfer area (30 x 30cm = 0.09m2)
dT = t1 - t2
= temperature gradient - difference - over the material (700 - 90 = 610)
Plugging the values into Fourier's Law we get:
= 1.05 / 0.009 * 0.09 * 610
= 6405 Watts
Assuming a 0.5kg log that has fallen out with a calorific energy value of 18MJ/kg (9MJ for 0.5kg) we can convert Watts (J/s) into how many seconds it takes to transfer through which looks like:
= 9000000 (Joules) / 6405 (Joules / Second) / 60 (seconds to minutes)
= 23 minutes
So it takes 23 minutes for a burning log to get the floor underneath to above 90 degrees above ambient when on a 9mm piece of glass assuming it doesn't crack under the temperature first.
Conversely a 10mm FC sheet works out at 1 hour 20 minutes for heat to transfer through.